Red Hot Cyber
Cyber security, cybercrime, hack news, and more
Menu
Antonio Piovesan : 4 October 2021 11:40
Author: Antonio Piovesan
Pubblication date: 28/09/2021
Great Britain, middle decades of the 19th century, times of unprecedented engineering ambitions.
Engineering, transportation, communications, architecture, science and manufacturing are in a feverish state of evolution. Inventors and engineers exploit new materials and new processes: it seems to be a period of endless inventions and innovations.
Supporta Red Hot Cyber attraverso
Steam engines are slowly replacing animals as a source of motive power. Iron ships begin to compete with sailing, rail networks expand rapidly, and the electric telegraph begins to revolutionize communications. Thriving science, engineering and new technologies guarantee limitless innovations.
Engineers, architects, mathematicians, astronomers, bankers, actuaries, workers, insurance agents, statisticians, navigators, anyone who needs calculations, relies on printed numerical tables for more than simple calculations.
Printed tables are calculated, copied, checked but composed by hand, but .. “Errare humanum est” .. humans are notoriously prone to error in nature and some people fear that undetected errors in a print could be possible source of economic or other disasters.
In this article we’ll tell the story of an idea, the story of a couple of precursors of their times, of the origins of automatic calculation or, as the title of a book I love by Silvio Hénin says, we will talk about “IL COMPUTER DIMENTICATO” (The forgotten computer).
But who are the main characters of this story?
English mathematician (Totnes, Devonshire, 1791 – London 1871), known especially for studies and projects relating to automatic calculating machines, including that of the “analytical engine”.
From 1828 to 1839, he was Lucasian Professor of Mathematics, a term used to identify the holder of the Lucasian Chair of Mathematics at the University of Cambridge, England. Lucasian professors were (among others) well-known names in Physics:
Given the importance of mathematical tables in his time (as mentioned for the economy, navigation, trade and more) and above all given the high number of calculation errors present in these tables, Babbage thinks (it is an idea born in 1812) to find a method by which mathematical tables can be calculated by a machine, not subject to the errors, fatigue and boredom that human beings paid to do the calculations manually (up to about the first half of the Twentieth century, “computer” was the English term to indicate a human being paid to do accounts, to make calculations).
Babbage is fascinated by the work on computing machines of Blaise Pascal and Gottfried Leibniz (Leibniz calculator, in English Stepped Reckoner), is very familiar with logarithmic tables and has a deep aversion to disorder.
Babbage is also interested in cryptography / cryptoanalysis: he realizes (maybe for a bet?) a method for “breaking” the ciphers carried out with the Vigenère cipher, a “polyalphabetic” system in that days called “the indecipherable cipher” (La chiffre indéchiffrable), attributed to the Frenchman Blaise de Vigenère (1523 – 1596). However, he will never publish his discovery (apparently because it was secreted by the UK government, that preferred to maintain the advantage of being able to decipher without the cipher knowing of the possibility of reading the plain text), which probably dates back to 1854 and that it will be attributed to him only in the twentieth century on the basis of the examination of his notes.
Augusta Ada King Byron, Countess of Lovelace (10 December 1815 – 27 November 1852) – English mathematician and writer, best known for her work on the “generic mechanical computer” proposed by Charles Babbage, the analytical engine.
Ada Byron is the only legitimate daughter of the poet Lord Byron and mathematician Anne Isabella Noel Byron. All of Byron’s other children are born out of wedlock, from other women. Byron separates from his wife one month after Ada’s birth and leaves England forever four months later. Byron commemorates the separation from her daughter in a poem whose beginning reads:
“Is thy face like thy mother’s, my fair child! ADA! Sole daughter of my house and heart?”
Ada’s father dies in Greece when Ada is only eight years old. Anne Isabella promotes Ada’s interest in mathematics and logic in an attempt to prevent her from developing her insanity and her perceived inclinations in her father. Despite this, Ada remains interested in her father, calling her two children Byron and Gordon. Upon her death, Ada is buried next to her father at her request. Although often ill in childhood, she keeps on studying assiduously and continuously.
Ada marries William King in 1835: King is named Earl of Lovelace in 1838, Ada then becomes Countess of Lovelace.
Her educational and social ventures bring her into contact with scientists such as Andrew Crosse, Charles Babbage, Sir David Brewster, Charles Wheatstone, Michael Faraday and author Charles Dickens, contacts that she uses throughout her life to further her education.
Ada describes her approach to knowledge as “poetic science” and defines herself as “Analyst (and metaphysics)”.
Babbage’s first machine, the Difference Engine No. 1, was designed to automatically calculate and tabulate mathematical functions called polynomials (Taylor series polynomials) which have very important general applications in mathematics and engineering. Babbage worked closely with Joseph Clement, a master toolmaker and designer in charge of making the mechanical parts.
Charles Babbage
Babbage presented the model of what he called the Difference Engine to the Royal Astronomical Society on June 14, 1823 in a paper entitled “Note on the application of machinery to the computation of astronomical and mathematical tables“. The first difference engine required 25,000 parts and would have weighted about four tons.
Modern replica of Difference Engine n.1 model created by Babbage in 1832
Construction was abruptly halted in 1833 when Clement knocked down tools and fired his workers following a dispute with Babbage overcompensation for moving Clément’s workshop closer to Babbage’s home.
The engine was never built approximately 12,000 unused precision parts were subsequently melted down as scrap. The project was a costly bankruptcy for the British government that had funded the venture. When the final bills were paid, the Treasury had spent £ 17,500 – equivalent to the cost of twenty-two steam locomotives built by Robert Stephenson’s factory in 1831 – a massive amount of money.
A portion of Babbage’s differential engine, assembled after his son’s death, using parts found in his laboratory
Details of the replica of the Difference engine no. 1 created in 1832
But … let’s try to understand why we are talking about differences, about difference engine.
A method based on the studies of mathematician Brook Taylor can be used to calculate the values of trigonometric or logarithmic functions.
Taylor proved that any mathematical function (sine, cosine, tangent, logarithm, etc.) can be approximated by a polynomial of the form:
ax⁶ + bx⁵ + cx⁴ + dx³ + ex² + fx + g
The higher the order of the polynomial (ie the greater is the larger exponent of x), the more accurate/precise the approximation will be. But what does this have to do with the cogwheels figures seen above? How can we use a purely mechanical instrument, the difference motor, “rotating” or rather “driven” by a manual crank to perform calculations?
Let’s see it with an example.
Let’s assume that the mathematical function that “we need”, that is, whose values we want to calculate, can be approximated with the polynomial
y = x² + 2x + 3
Let’s calculate y values according to increasing x values from 1 to 6
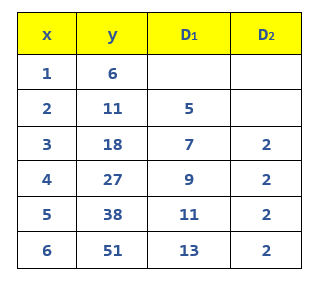
For values from 1 to 6 of x we calculated the values of column y; in column D1 we calculated the difference between a value of y and the previous one; in column D2 we calculated the difference between a value of D1 and the previous one.
It can be noted that for the polynomial of order 2 (the X with the highest exponent is raised to the second) the second difference returns an always constant value…. For a polynomial of order 6, for example, our example table would have 8 columns: column x, column y followed by 6 columns D1 D2 D3 D4 D5 D6.
Using previous table, we can calculate values of the polynomial by not calculating a multiplication (x multiplied by itself) followed by two additions, but calculating only additions … Example:
X = 7D2 = 2D1 = 15Y = 15 + 51 = 66Test: 66 = 7² + (7 x 2) + 3 = 49 + 14 + 3 = 49 + 17 = 66X = 8D2 = 2D1 = 17Y = 17 + 66 = 83Test: 83 = 8² + (8 x 2) + 3 = 64 + 16 + 3 = 64 + 19 = 83
Babbage was aware, as mentioned, of Taylor’s studies, therefore, he designed an engine that could exploit the procedure just described, capable of transforming the approximate calculation, for example, of values of logarithmic or trigonometric functions into simple sums. The calculator would only have to turn a crank and with each click of the crank, a new successive value of the variable y would be calculated.
Babbage’s project was based on 7 columns, y D1 D2 D3 D4 D5 D6 represented on 7 columns of cogwheels: each wheel was divided into 10 sectors (from 0 to 9) and each column had 6 wheels to be able to represent numbers from 0 to 999’999. The wheels of each column meshed with the corresponding wheels of the other in order to report the sums from column D6 to D5, from D5 to D4 and so on up to the last column y. An “ad hoc” mechanism ensured that carryovers were taken into account when the sum exceeded 10.
A subsequent idea of Babbage was to equip differences engine with printer , so as not to have to annotate the values calculated for the variable y each time.
In 1834, the difference engine n. 1 project was stalled due to lack of government funding; Babbage devised a new, more ambitious engine, later called the Analytical Engine, an all-purpose programmable “computer science” engine. The analytical engine can be thought of as a logical “quantum leap” and its design can be seen as one of the most surprising intellectual achievements of the 19th century.
The analytical engine presented many essential principles found in modern digital computers and its conception marks the transition from mechanized arithmetic (Pascal’s and Leibniz’s calculators) to complete general calculus. Babbage can be considered ‘the first pioneer of computers’ or of programmable automatic computing for this project, which has never been realized in practice.
“ … The drawings of the Analytical Engine have been made entirely at my own cost: I instituted a long series of experiments for the purpose of reducing the expense of its construction to limits which might be within the means I could myself afford to supply. I am now resigned to the necessity of abstaining from its construction… ”
The analytical engine had many essential features found in the modern digital computer. It was programmable using punch cards, an idea borrowed from the Jacquard loom used for weaving complex patterns in fabrics; it had a “Store” where intermediate numbers and results could be stored and a separate “Mill” where arithmetic processing was performed. It had an internal repertoire of the four arithmetic functions and could directly perform multiplications and divisions. It was also capable of functions for which we have the modern names of conditional jump / if, switch, loop (iteration) although Babbage never used these terms.
The engine had a variety of output types including paper printing, punch cards, graphic plotting and automatic production of stereotypes (trays of soft material into which results were imprinted that could be used as molds to make printing plates).
Punch cards
The logical structure of the “Analytical Engine” was essentially the same as that which dominated computer design in the electronic age: the separation of memory (the “Store”) from the central processor (the “Mill”), the serial operation through an iterative cycle of execution of calculations and structures for the input and output of data and instructions.
“The Analytical Engine weaves algebraic patterns just as the Jacquard loom weaves flowers and leaves.”
In 1833 Babbage met Ada Lovelace, daughter of the well-known British poet Lord Byron, at a party. Lovelace, just seventeen, had a mathematical background that was unusual for a woman at the time. Ada was enchanted by Babbage’s work on computing machines and over time became an enthusiastic supporter of Babbage.
Analytical engine model
Babbage visited Turin in 1840 to participate in the second Congress of Italian scientists at the Academy of Sciences. He discussed his ideas with Italian mathematicians, including Luigi Menabrea. During Babbage’s visit, Menabrea collected all the necessary material to describe the analytical engine and published it in October 1842 (in France) in french language.
The idea of the conditioned jump, the ability to change the sequence of operations automatically based on the intermediate numerical result obtained at a particular moment by the analytical engine, was the result of a conversation that took place in Turin between Babbage and the mathematician Ottaviano Fabrizio Mossotti.
In 1843 Ada Lovelace published that article by the Italian engineer Menabrea translated from French into English. She added to it extensive notes by her own that made the article in the English version three times longer than the original French article. The notes included a description of the steps that the “analytical engine” would have taken to solve some mathematical problems – procedures we would now call programs – the first published descriptions of that genre (we are referring to note G – the computation of Bernoulli numbers).
Lovelace hypothesized that the engine could go beyond numbers and more generally manipulate symbols. She “noticed” that numbers could represent entities other than mere quantities … letters of the alphabet … musical notes … and that by manipulating the numbers, computing engines could extend their powers beyond the world of mathematics. Considering developments in the twentieth century, this notion may seem prophetic: Babbage seems not to have come to imagine this clearly, most likely he had not understood the potential of his project.
Ada was one of the few people who fully understood Babbage’s ideas: there are, in fact, clues (monograph by Menabrea) where Ada probably suggests the use of Jacquard Loom punch cards for the analytical engine designed by Babbage.
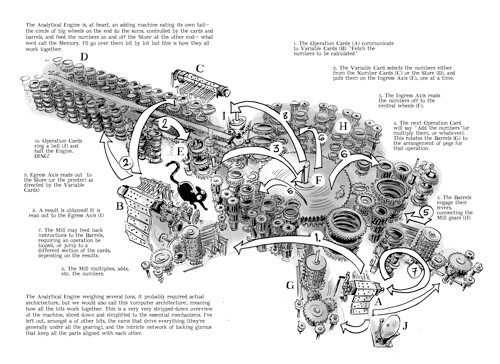
We talked about Mill (arithmetic unit), Store (memory unit) and punch cards “borrowed” from the Jacquard loom: let’s see how this is based and constitutes a logical evolutionary leap of the differential engine n.1.
There were four types of punch cards:
The cards, read in sequence by the engine, allowed its programmability.
If we wanted to calculate y values of the following equation using the analytical engine
Y = 34 * (27 + 9) / 12
Numbers 34, 27, 9 and 12 should be recorded in 4 columns of the Store. Let’em be V1, V2,V3 and V4.
For this we will use four number cards. Columns V5 V6 and V7 would be used for the intermediate results and for the final result:
– We put with the punched cards V2 = 27 and V3 = 9 in the Mill.
– 27 + 9 = 36 which we will put in V5
– V6 receives the result of V5 / V4 36/12 = 3
– The Mill multiplies V1 * V6 34 * 3 = 102 and transfers 102 to V7
For this calculation we will use:
– Four numbers cards
– Three operations cards (one for addition, one for division and one for multiplication)
– Nine variables cards.
More cards would be needed to conduct the final printing of the result.
Much more complex examples can be found in Menabrea’s article translated by Ada Lovelace into English.
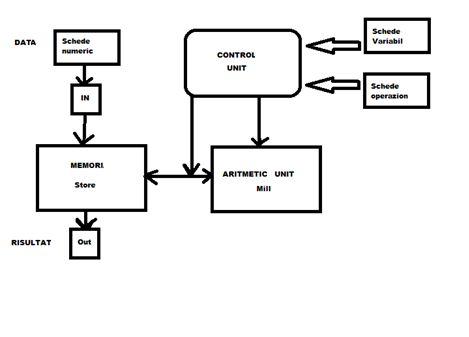
Babbage Architecture (Analytical Engine)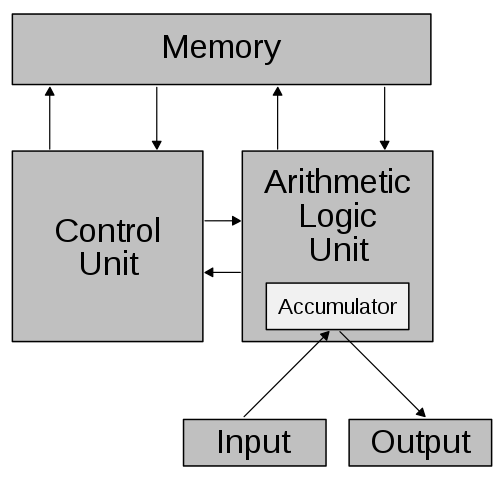
Von Nuemann Architecture: in Von Neumann “input” is based on both DATA and PROGRAMME
As Babbage perfected the mechanics of the analytical engine, he also sought to see how he could simplify the design of the difference engine. Between 1847 and 1849 he designed a new engine, the Difference Engine No. 2. The new design benefited from many of the techniques developed for the more demanding analytical engine.
The new design was elegant and efficient, requiring a third of the number of machine parts to the No. 1 for more computing power. With 8,000 parts, the machine would weigh five tons and measure eleven feet in length and seven feet in height. Babbage made no attempt to build such an engine. This is the project that was actually built and completed in 2002, and is the first of Babbage’s engine projects to have been built in its entirety.
Babbage failed to build a complete engine despite his wealth, social standing, government funding, a decade of R&D (let’s say now) and the best of British engineering.
The reasons are still debated and there are many facts to be considered:
these are all factors to consider.
Babbage was a character of great principle but easily offended and prone to strong public criticism from those he considered his enemies.
Babbage was also a very bad “marketer” of himself, of his projects. He disdained lecturing on his work and neither proclaimed nor promoted the mathematical potential of his machines. Consequently, they were judged primarily for their “practical utility” for producing error-free tables, and the experts of the time disagreed that there was a real need for new tables with very high precision: some argued that the existing tables were already sufficiently accurate and that there was no economic justification for the large capital costs of building its huge machines. Others wondered whether the twenty, thirty, or fifty digits of accuracy Babbage insisted were justified when measurements could be made to no more than a few decimal places.
Differential engine # 2 model
The 19th century movement to automate the computation failed and the movement largely died with Babbage in 1871. There is no continuous line of development from Babbage to the present day, and many of the principles embodied in his work have been reinvented by the pioneers of the electronic age, largely in ignorance of his work. Although the legend of his work was never lost, it was only in the 1970s that his designs were studied in detail and the scale of his accomplishments emerged more clearly.
Babbage’s work is associated with that of the one who is considered the first computer programmer, Ada Augusta Lovelace AAL to whom the French CII Honeywell Bull company under contract for the United States Department of Defense (DoD) at the end of the 70s dedicated a new programming language called ADA.
Insights
https://www.redhotcyber.com/post/genesi-dell-informatica-ed-evoluzione-dell-uomo-nel-digitale
https://www.cultureofcybersecurity.com/cybear-family/ada-cybear/
https://www.cultureofcybersecurity.com/
Antonio Piovesan
