Red Hot Cyber
Sicurezza Informatica, Notizie su Cybercrime e Analisi Vulnerabilità
Autore: Roberto Campagnola
Data Pubblicazione: 07/04/2022
Link al documento PDF: Documento originale
Nel corso di questa rubrica abbiamo più volte rimarcato quanto sia peculiare la meccanica quantistica rispetto alla nostra “realtà” e uno dei fenomeni più caratteristici è l’entanglement.
Due particelle, o più in generale due o più sistemi fisici, si definiscono entangled (intrecciate) quando i loro stati sono descrivibili come combinazione o sovrapposizione di più stati e sono correlati, cioè misurando il valore di una grandezza di un sistema, il valore della stessa grandezza per l’altro sistema è istantaneamente determinato.
Negli anni in cui la meccanica quantistica era agli inizi, gli studi sui fenomeni solo apparentemente in contrasto con il “comune sentire” portarono alla formulazione di alcuni paradossi: tra i più famosi quello conosciuto come paradosso EPR, che avrebbe influenzato la nostra idea sul principio di località (in fisica secondo il principio di località gli oggetti distanti non possono avere influenza istantanea l’uno sull’altro).
Il paradosso fu risolto grazie a John Bell e il suo teorema, in cui si dimostra che la realtà è non locale e che i postulati della meccanica quantistica, seppur apparentemente assurdi, non sono in contraddizione con la realtà che, lo ricordiamo, nella sua essenza è quantistica.
Dati due sistemi quantistici A e B, definiti con i rispettivi spazi di Hilbert HA , HB, lo spazio di Hilbert globale è definito secondo i postulati della meccanica quantistica dal prodotto tensoriale dei singoli spazi
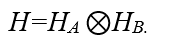
Dati i vettori di stato dei sue sistemi
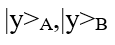
lo stato globale del sistema è definito da
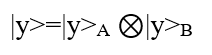
Stati di questo tipo sono chiamati stati separabili.
Due sistemi possono non essere esprimibili come stati singoli definiti e lo stato globale non è separabile, ma possono verificarsi casi in cui lo stato globale è dato dalla somma, quindi dalla sovrapposizione dei due vettori di stato, di cui abbiamo parlato nel secondo numero della nostra rubrica.
Possiamo dire che lo stato non è separabile nei singoli stati degli spazi di Hilbert di A e B. Supponiamo che Alice sia una osservatore per il sistema A e Bob per il sistema B; se Alice effettua una misura nella base dei possibili vettori {|0>, |1>}, allora i risultati possibili sono due con probabilità uguale:
Nel primo evento ogni successiva misura di Bob darà sempre il risultato 1, mentre nel secondo evento Bob otterrà sempre 0. Il sistema di Bob, quindi, è stato modificato dalla misura di Alice effettuata localmente sul sistema; e questo rimane vero anche se i due sistemi sono separati spazialmente, indipendentemente dalla distanza.
Bisogna sottolineare un punto fondamentale: il risultato della misura di Alice è casuale, non può scegliere quale risultato ottenere e quindi non ci può essere trasferimento di informazione a Bob. Il principio di causalità è quindi rispettato.
Einstein, Podolsky e Rosen studiando il fenomeno dell’entanglement e le sue conseguenze, nel 1935 pubblicarono un articolo ( “Can Quantum-Mechanical Description of Physical Reality be Considered Complete?” , divenuto famoso come paradosso EPR) in cui si rigettavano alcuni risultati, e si definiva la meccanica quantistica una teoria incompleta; la teoria come era stata formulata fino ad allora non poteva essere corretta, perché alcuni risultati, in particolare l’entanglement, contrastavano con i principi di realtà e di località, considerati evidenti.
Ci dovevano essere delle variabili nascoste, ancora ignote che rimettevano in ordine le cose, e la rendessero fortemente deterministica. Il paradosso fu risolto nel 1964 da John Stuart Bell, che grazie alla formulazione delle cosiddette disuguaglianze di Bell e alle verifiche sperimentali che ne seguirono, dimostrò come la realtà è non locale e che una teoria locale a variabili nascoste non può replicare i risultati della meccanica quantistica.
Nella formazione dei qubit si possono costruire i cosiddetti stati di Bell, stati di due qubit totalmente entangled descritti dai vettori di stato:
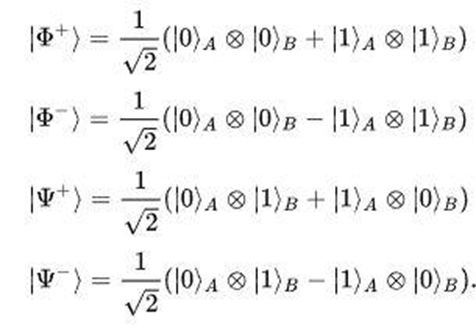
Il modo più semplice per creare uno stato di Bell è utilizzare un gate Hadamard e un gate CNOT, di cui abbiamo già parlato nel terzo numero sui circuiti.
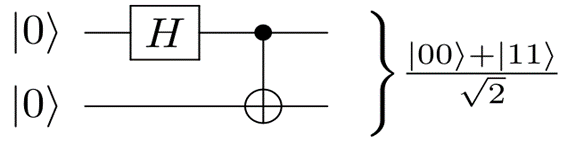
Nell’immagine è illustrata la costruzione dello stato indicato come |Φ+> a partire da due qubit |00>.
Lo stato |00> viene trasformato nella sovrapposizione
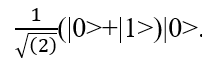
Su questo stato agisce il CNOT che inverte il secondo qubit solo quando il primo assume il valore 1, dando quindi il risultato
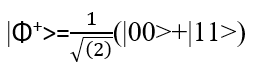
Abbiamo adesso l’occasione per dare un primo sguardo al Composer del servizio IBM, che offre la possibilità di accedere ai server dei loro computer quantistici e comporre i primi circuiti. Costruiremo proprio il circuito descritto dallo stato |Φ+>. Possiamo impostare e simulare un circuito quantistico affidandoci ad una interfaccia grafica (è disponibile anche un compilatore per costruire il circuito attraverso Qiskit ). Per usufruire dei servizi quantum computing di IBM è necessario connettersi a https://quantum-computing.ibm.com, effettuare l’iscrizione (questo per poter utilizzare il computer quantistico di IBM e non solo la fase di simulazione),cliccare sull’icona in alto a sinistra
; posizionarsi su Composer → File → New e nominare il file sostituendo la dicitura Untitled circuit; possiamo trascinare i gate sui “fili “ corrispondenti ai qubit che abbiamo inizializzato. Il composer va pensato come una “partitura” musicale in cui da sinistra a destra progredisce il tempo di calcolo quantistico, più che ad una disposizione spaziale degli elementi circuitali.
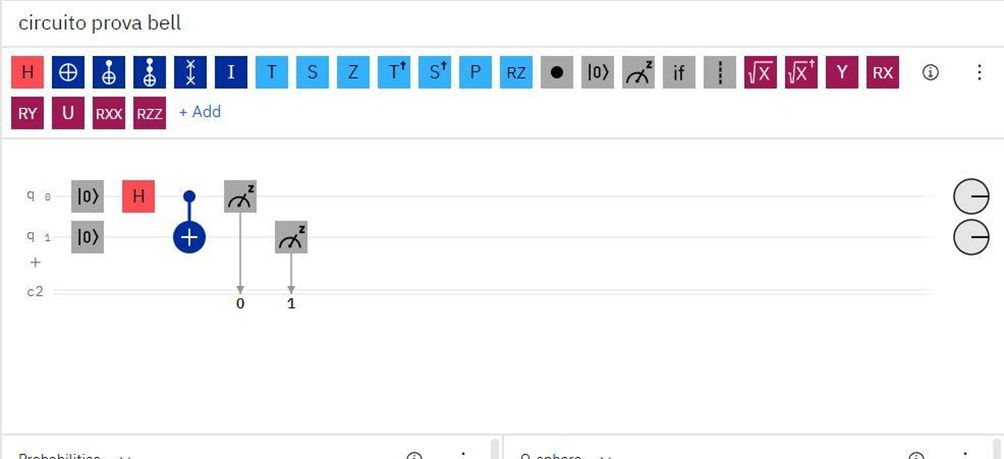
Dall’elenco di gate disponibili in alto, spostiamo un primo gate di Hadamard sul qubit 0, successivamente importiamo un gate CNOT, e due gate di misura sui qubit 0 e 1. Misurare un qubit significa farlo interagire con l’ambiente esterno, per poter trasformare i risultati quantistici in un registro di bit classico e quindi misurabile, dall’utente cioè da noi.
Interfaccia grafica per la creazione dello stato di Bell |Φ+> sul composer IBM
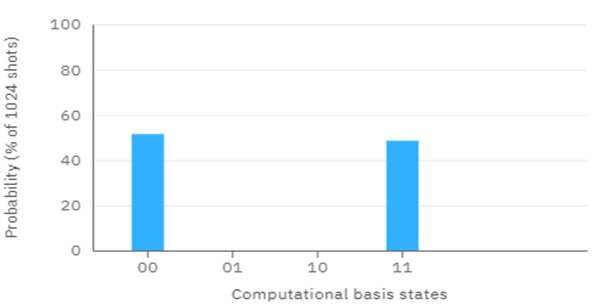
Nel riquadro in basso a sinistra otteniamo le probabilità dei risultati ottenuti. Non sempre in una misura reale le probabilità corrispondono precisamente a quelle aspettate, questo a causa degli errori e delle imprecisioni intrinseche del processo di misura dei Quantum Computer: la minimizzazione degli errori nel calcolo è uno dei passaggi fondamentali per un QC.
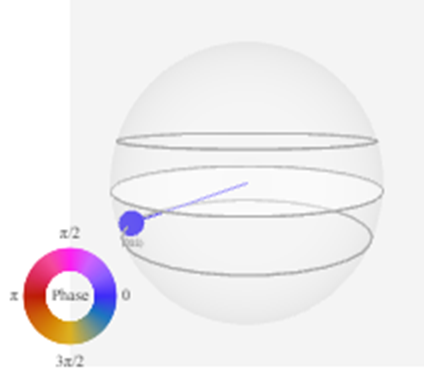
Nel riquadro in basso a destra abbiamo la rappresentazione per mezzo della Q-sphere, che fornisce una informazione grafica del sistema di qubit che stiamo studiando. E’ importante rimarcare che, sebbene la Q-sphere presenti delle analogie con la sfera di Bloch (di cui abbiamo già parlato nel secondo numero), in realtà fornisce una rappresentazione globale del sistema e non relativa ai singoli qubit. Nella sfera di Bloch abbiamo una descrizione in cui ogni qubit è studiato e rappresentato singolarmente, nella Q-sphere abbiamo una rappresentazione globale dei qubit e degli effetti che si producono quando più qubit sono accoppiati in un circuito quantistico.
Dalla simulazione ottenuta vediamo che dopo aver misurato il primo qubit, si hanno due risultati possibili per il secondo qubit, corrispondenti alle probabilità di sovrapposizione che avevamo nello stato
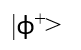
ricordiamo che il coefficiente
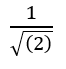
della combinazione lineare va elevato al quadrato per avere la probabilità dei singoli stati, quindi ½.
Questo è solo uno dei molti circuiti che possiamo creare sull’ IBM Composer, vi invitiamo a provarne più che potete; IBM fornice una guida dettagliata con molti esempi e i principi fondamentali su cui si basa la computazione quantistica.
Nel prossimo numero vedremo come la meccanica quantistica possa essere sfruttata nel campo della comunicazione e della crittografia quantistica.
Fonti
Ti è piaciuto questo articolo? Ne stiamo discutendo nella nostra Community su LinkedIn, Facebook e Instagram. Seguici anche su Google News, per ricevere aggiornamenti quotidiani sulla sicurezza informatica o Scrivici se desideri segnalarci notizie, approfondimenti o contributi da pubblicare.
Innovazione
Cybercrime
Vulnerabilità
Innovazione
Cyber Italia