Articolo di: Emanuele Buchicchio
27/08/2020
Gli schemi di crittografia tradizionali possono essere utilizzati per esternalizzare l’archiviazione dei dati sul cloud senza compromettere la riservatezza utilizzando soluzioni Zero-Knowledge encryption in cui i dati sono presenti sul cloud solo in forma cifrata ed il gestore del servizio cloud non ha accesso alle chiavi di cifratura.
Il limite di questo approccio è che i dati cifrati non possono essere utilizzati per eseguire elaborazioni senza prima decifrarli.
In questo scenario un servizio cloud sicuro non a accesso ai dati in chiaro e deve necessariamente richiedere a un utente di scaricare i propri dati crittografati, decifrarli localmente, eseguire i calcoli necessari, cifrare localmente il risultato dell’elaborazione ed caricarlo nuovamente sul cloud.
La strategia Zero-Knowledge non è utilizzabile quando è necessaria l’elaborazione dei dati sul cloud.
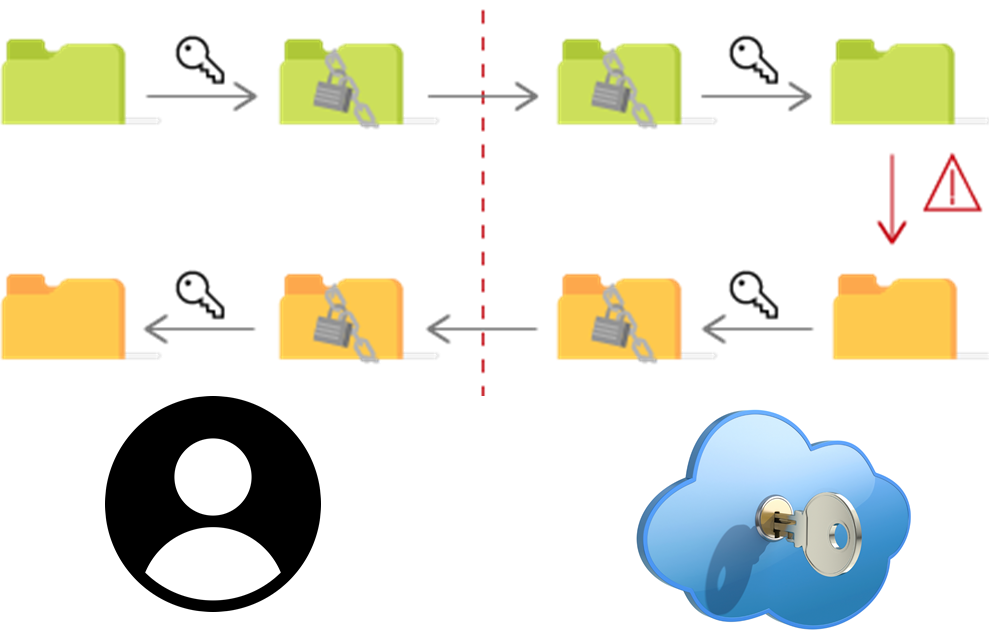
In questo scenario il fornitore del servizio deve poter decifrare i dati per eseguire le elaborazioni richieste e quindi deve necessariamente avere accesso alle chiavi di cifratura.
Anche in presenza di processi implementati e certificati secondo i migliori standard di sicurezza in questo scenario la sicurezza è basata sulla fiducia riposta nel gestore del servizio cloud.
La crittografia omomorfica risolve questo problema, poiché consente al servizio cloud di eseguire i calcoli direttamente sui dati cifrati senza la possibilità di accedere ai dati in chiaro.
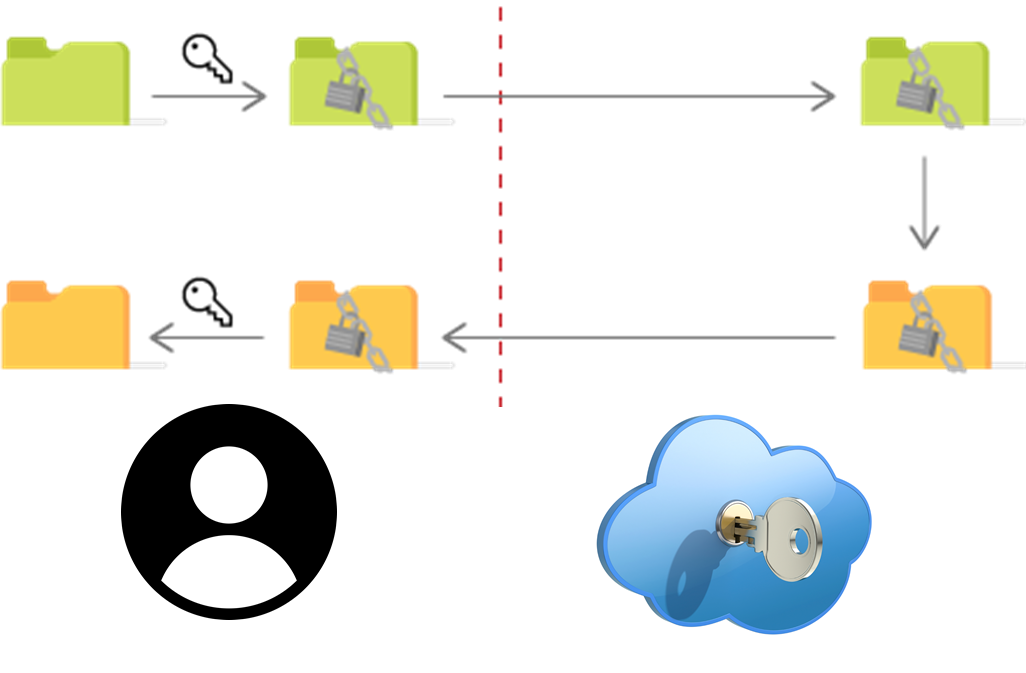
L’utilizzo della crittografia omomorfica permette di sostituire la fiducia nel fornitore con la garanzia matematica offerta dalla crittografia: i dati non saranno mai disponibili in chiaro al gestore del servizio e le chiavi di cifrature sono note solo all’utente e non vengono mai caricate sul cloud.
In settori altamente regolamentati, come l’assistenza sanitaria, la crittografia omomorfica può essere utilizzata per abilitare nuovi servizi rimuovendo le barriere sulla privacy che inibiscono la condivisione dei dati.
Ad esempio, l’analisi predittiva nell’assistenza sanitaria può essere difficile da applicare a causa di problemi di privacy ei dati sanitari, ma se il fornitore di servizi di analisi predittiva può operare su dati crittografati, tali problemi di privacy vengono ridotti.
La crittografia omomorfica (homomorphic encryption – HE) è una forma di crittografia che consente di eseguire calcoli sui dati cifrati (ciphertexts), generando un risultato crittografato che, una volta decrittografato, corrisponde al risultato delle operazioni come se fossero state eseguite sui dati in chiaro (plaintext).
L’aggettivo “omomorfico” si riferisce all’omomorfismo in algebra: le funzioni di crittografia e decrittazione possono essere pensate come omomorfismi tra strutture algebriche.
L’intuizione di avere un crittosistema pienamente omomorfo risale al 1978 e viene menzionata nell’articolo [ R. L. Rivest, L. Adleman, M. L. Dertouzos,On data banks and privacy homomorphism,in “Foundations of Secure Computation”, Academic Press, 1978, 169-180.] pubblicato pochi mesi dopo la prima implementazione di RSA.
Gli autori suggeriscono la possibilità di creare un crittosistema pienamente omomorfo con l’obiettivo di aumentare la privacy sui dati, ma non riescono ad ipotizzare una implementazione.
Questo risultato è stato raggiunto solo molti anni più tardi grazie al lavoro di Craig Gentry [1,2] nel 2009.
Tra le varie implementazioni di sistemi di crittografia omomorfica quelle di maggiore interesse applicativo sono i quelli che permettono di eseguire qualsiasi sequenza arbitraria di operazioni sui dati cifrati e poi decifrare il risultato. I sistemi che hanno questa caratteristica sono definiti fully homomorphic encryption (FHE).
Purtroppo dal punto di vista pratico l’implementazione di un sistema di crittografia FHE pone molte difficoltà sia dal punto di vista della capacità di calcolo necessaria sia dal punto di vista della precisione numerica. Per un approfondimento sulla teoria alla base degli algoritmi FHE suggerisco due riferimenti dedicati agli appassionati di matematica e crittografia:
Il problema dal punto di vista dello sviluppatore medio è trovare una libreria utilizzabile all’interno di una applicazione reale. Un elenco aggiornato delle implementazioni disponibili è mantenuto dal consorzio www.HomomorphicEncryption.org però molte delle librerie hanno un taglio decisamente accademico e richiedono una conoscenza approfondita della materia e competenze matematiche avanzate.
Tra le librerie utilizzabili anche dai non addetti ai lavori io ho scelto SEAL (https://www.microsoft.com/en-us/research/project/microsoft-seal/). Il progetto è attivamente mantenuto e personalmente mi sono trovato piuttosto bene nel realizzare alcune applicazioni di prova seguendo la documentazione e gli esempi.
Ad esempio ho trovato molto utile (anche se con qualche bug) il tutorial “Tracker Lab” (https://aischool.microsoft.com/en-us/responsible-ai/learning-paths/homomorphic-encryption-la) in cui viene costruita una semplice applicazione dimostrativa.
Il risultato di questo esercizio è su GitHub https://github.com/emanbuc/SEAL_TrackerLab
Altre applicazioni dimostrative e tutorial (più recenti) sono pubblicati su https://www.microsoft.com/en-us/ai/ai-lab-he
Seguici su Google News, LinkedIn, Facebook e Instagram per ricevere aggiornamenti quotidiani sulla sicurezza informatica. Scrivici se desideri segnalarci notizie, approfondimenti o contributi da pubblicare.
