Autore: Roberto Campagnola
Data Pubblicazione: 6/02/2022
Nel 1996, durante la sua attività di ricerca presso la IBM, il fisico David DiVincenzo pubblicò un articolo intitolato “Topics in Quantum Computing” in cui delineò 5 requisiti minimi necessari per la realizzazione di una macchina a computazione quantistica.
 Christmas Sale -40% 𝗖𝗵𝗿𝗶𝘀𝘁𝗺𝗮𝘀 𝗦𝗮𝗹𝗲! Sconto del 𝟰𝟬% 𝘀𝘂𝗹 𝗽𝗿𝗲𝘇𝘇𝗼 𝗱𝗶 𝗰𝗼𝗽𝗲𝗿𝘁𝗶𝗻𝗮 del Corso "Dark Web & Cyber Threat Intelligence" in modalità E-Learning sulla nostra Academy!🚀
Fino al 𝟯𝟭 𝗱𝗶 𝗗𝗶𝗰𝗲𝗺𝗯𝗿𝗲, prezzi pazzi alla Red Hot Cyber Academy. 𝗧𝘂𝘁𝘁𝗶 𝗶 𝗰𝗼𝗿𝘀𝗶 𝘀𝗰𝗼𝗻𝘁𝗮𝘁𝗶 𝗱𝗲𝗹 𝟰𝟬% 𝘀𝘂𝗹 𝗽𝗿𝗲𝘇𝘇𝗼 𝗱𝗶 𝗰𝗼𝗽𝗲𝗿𝘁𝗶𝗻𝗮.
Per beneficiare della promo sconto Christmas Sale, scrivici ad [email protected] o contattaci su Whatsapp al numero di telefono: 379 163 8765.
Se ti piacciono le novità e gli articoli riportati su di Red Hot Cyber, iscriviti immediatamente alla newsletter settimanale per non perdere nessun articolo. La newsletter generalmente viene inviata ai nostri lettori ad inizio settimana, indicativamente di lunedì. |
I primi quattro criteri valgono anche per i computer classici perché non vogliamo esser limitati in termini di architetture o possibili operazioni da svolgere, mentre l’ultimo criterio è specifico per i computer quantistici.
Abbiamo visto che i principi fondamentali su cui si basa il computer quantistico sono i principi della sovrapposizione coerente di stati, e dell‘entanglement.
Lo stato di un sistema quantistico può essere descritto da una combinazione lineare a coefficienti complessi di vettori in uno spazio di Hilbert:
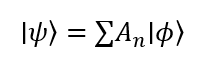
Finché non avviene il processo di misura, il sistema si trova contemporaneamente in tutti i possibili valori della grandezza, e solo quando si effettua una misura si ottiene uno dei possibili risultati, ognuno secondo una differente probabilità, data dal modulo quadro del coefficiente complesso della combinazione lineare.
Si presentano casi in cui lo stato di un sistema quantistico non è descritto da una sovrapposizione coerente di stati, ma da una miscela statistica, nel caso in cui si stiano studiando sistemi quantistici indipendenti. Alla “miscela statistica” è associata una probabilità classica, cioè una probabilità che nasce dalla nostra mancata conoscenza di tutte le sue condizioni e che quindi ci porta dover ricorrere alla statistica per poterne descrivere lo stato e l’evoluzione. A differenza della probabilità quantistica che è una probabilità intrinseca dei sistemi quantistici.
Questo fenomeno si verifica in particolari condizioni quando due o più stati possono essere considerati sottosistemi di un sistema quantistico più ampio, e il cui stato può essere descritto solo come sovrapposizione di più stati. Tale condizione, che non ha alcun corrispettivo nel mondo classico, porta a diversi fenomeni a prima vista contro intuitivi ma perfettamente verificati e spiegabili secondo la fisica quantistica: se per esempio si costruisce uno stato entangled a partire da due stati di due particelle legate tra loro, la misura di una variabile su una particella influenzerà istantaneamente la grandezze dell’altra, indipendentemente dalla distanza che le separa.
L’entanglement portò alla formulazione del paradosso EPR da parte di Einstein, Podolsky e Rosen per mettere in luce l’apparente incompletezza della meccanica quantistica, e la necessità di una sua confutazione. In realtà il paradosso fu spiegato nel 1964 grazie alle famose disuguaglianze di Bell, che portarono alla conclusione che in alcuni aspetti la meccanica quantistica è una teoria che non rispetta il principio di località.
I qubit di un computer, sono quindi oggetti estremamente “delicati”: ogni interazione con l’ambiente esterno ne altera irrimediabilmente lo stato, portando al fenomeno del collasso della funzione d’onda, che è stato spiegato usando la decoerenza quantistica. Per esempio un debole campo magnetico o un casuale impulso di microonde possono indurre l’inversione dei qubit (bit-flip) invertendo le loro possibilità di essere |0⟩ e |1⟩ rispetto agli altri qubit, o l’inversione di fase (phase-flip), la trasformazione della relazione matematica tra i loro due stati.
Quando i qubit di un sistema quantistico raggiungono la decoerenza, l’informazione in essi contenuta è persa, ed è quindi necessario mantenere la fase di sovrapposizione coerente il più a lungo possibile.
Nella computazione classica per evitare una perdita di informazione è naturale ricorrere alla ridondanza e creare delle copie identiche dei bit contenenti ognuna la stessa informazione. Si possono così eseguire le operazioni, avendo a disposizione più copie degli stessi bit in caso di errori, difetti o mancanze. Nel mondo quantistico, questa tecnica non è possibile a causa del teorema del no-cloning quantistico che in una sua versione semplificata impedisce la creazione di stati quantistici sconosciuti a priori.
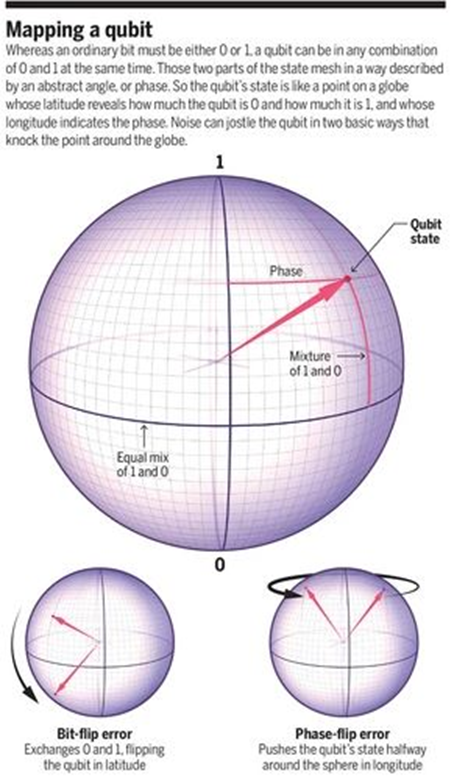
Rappresentazione di alcuni errori possibili nella computazione quantistica
Sono stati sviluppati negli anni diversi algoritmi quantistici di correzione degli errori; uno di essi che fa uso di un processo simile alla versione classica, è stato ideato da Peter Shor, di cui abbiamo già parlato. In tale algoritmo si utilizzano più qubit portatori per salvaguardare l’informazione di un singolo qubit: si fa in modo che l’informazione venga codificata su stati entangled di più qubit, in modo tale che se si verifica un errore gli stati logici sono mappati in altri stati ortogonali.
Successivamente, a questi stati si associa anche una osservabile la cui misura fornisce informazioni in quale sottospazio si trovi lo stato: sapremo quindi che si è verificato un errore senza però ricevere alcuna informazione su di esso e senza dover effettuare una misura sul qubit; sappiamo in fatti che la misura in meccanica quantistica è un processo altamente “distruttivo” perché porta per definizione al collasso della funzione d’onda.
Lo sviluppo di algoritmi di correzione degli errori e gli studi per aumentare il tempo di decoerenza, sono in costante sviluppo: ad esempio nei computer quantistici a super conduttori, che rappresentano le architetture più usate e ritenute più promettenti, i tempi di decoerenza sono passati dell’ordine dei nanosecondi alle centinaia di microsecondi, che rappresenta un salto di numerosi ordini di grandezza.
Nel prossimo numero della nostra rubrica esamineremo le architetture più usate e i tipi più diffusi di computer quantistici..stay tuned, al prossimo mese!
Fonte
Photo credit:Cho, Adrian (2020).No room for error. Science, 369(6500)
Ti è piaciutno questo articolo? Ne stiamo discutendo nella nostra Community su LinkedIn, Facebook e Instagram. Seguici anche su Google News, per ricevere aggiornamenti quotidiani sulla sicurezza informatica o Scrivici se desideri segnalarci notizie, approfondimenti o contributi da pubblicare.
Hacking
Vulnerabilità
Vulnerabilità
Cyberpolitica
Cultura