Red Hot Cyber
La cybersecurity è condivisione. Riconosci il rischio, combattilo, condividi le tue esperienze ed incentiva gli altri a fare meglio di te.
Roberto Campagnola : 5 Dicembre 2021 17:19
Autore: Roberto Campagnola
Data Pubblicazione: 5/12/2021
Nell’informatica classica l’architettura principale dei calcolatori è basata sulle porte logiche o gate, espresse da circuiti elettrici con cui, mediante l’algebra booleana possono essere compiute le operazioni logiche necessarie a “costruire” le operazioni matematiche e non solo che il calcolatore è in grado di svolgere.
Vorresti toccare con mano la Cybersecurity e la tecnologia? Iscriviti GRATIS ai WorkShop Hands-On della RHC Conference 2025 (Giovedì 8 maggio 2025)
Se sei un ragazzo delle scuole medie, superiori o frequenti l'università, oppure banalmente un curioso di qualsiasi età, il giorno giovedì 8 maggio 2025 presso il teatro Italia di Roma (a due passi dalla stazione termini e dalla metro B di Piazza Bologna), si terranno i workshop "hands-on", creati per far avvicinare i ragazzi alla sicurezza informatica e alla tecnologia. Questo anno i workshop saranno:
Supporta RHC attraverso:
Ti piacciono gli articoli di Red Hot Cyber? Non aspettare oltre, iscriviti alla newsletter settimanale per non perdere nessun articolo.
Nella computazione quantistica si usa la stessa “linea di pensiero”: si usa sempre la logica circuitale ma con alcune differenze notevoli, sia di implementazione pratica sia di formalismo e rappresentazione.
Possiamo descrivere i gate quantistici come qualsiasi operazione che può cambiare lo stato dei qubit, e che è necessaria per compiere le istruzioni di un dato algoritmo.
Per comprendere il funzionamento delle porte logiche, la loro rappresentazione e i loro effetti sui qubit è necessario un livello di astrazione non comune, come del resto per tutta la computazione quantistica.
Abbiamo spiegato che i qubit sono rappresentati e possono essere studiati sotto forma di vettori un uno spazio vettoriale complesso, allo stesso modo le porte logiche sono rappresentate da matrici unitarie, matrici la cui la matrice trasposta coniugata è uguale alla sua inversa. L’operazione di trasposizione di una matrice, scambia le righe con le colonne, mentre la coniugazione di un numero complesso cambia il segno della parte immaginaria (dato il numero complesso z=a + ib, il complesso coniugato è definito come z* = a – ib). Definita U matrice quadrata nel campo complesso, deve essere che UU*=U*U= I, con I la matrice identità. La richiesta della unitarietà delle matrici associate ai gate discende dai postulati fondamentali della meccanica quantistica.
Le matrici unitarie sono infinite, quindi abbiamo infinite operazioni che possono essere applicate a qubit singoli. Tuttavia possiamo studiare le proprietà fondamentali attraverso un numero più ristretti di operazioni e quindi i gate quantistici (chiamati gate universali).
Abbiamo visto come lo stato fondamentale di singolo qubit sia espresso dal vettore
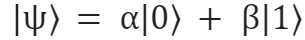
a questo possiamo applicare i gate logici che serviranno per programmare, come vedremo nelle lezioni seguenti, il calcolatore quantistico ed eseguire delle operazioni.
Senza perdere in generalità, riportiamo solo alcuni esempi di gate quantistici,
Tra i più importanti, troviamo sicuramente le tre matrici di Pauli, già usate in meccanica quantistica per descrivere l’interazione dello spin di una particella con un campo elettromagnetico esterno. Le tre matrici possono essere indicate come:
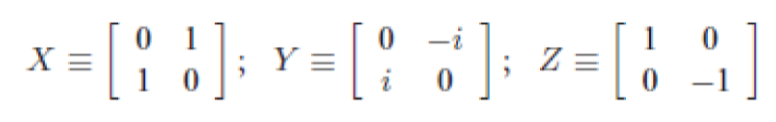
Tali matrici, se applicate ad un qubit ne rappresentano una rotazione di 180° nella sfera di Bloch lungo il rispettivo asse.
Il gate X, è inoltre usato per implementare l’operazione di NOT, in quanto se applicato al vettore
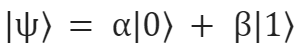
ed eseguendo il prodotto righe per colonne, mappa lo stato |0> nello stato |1>, e viceversa.
Un altro gate di fondamentale importanza è il gate di Hadamard: anche questo gate di rotazione di lungo un asse, ma la rotazione avviene lungo l’asse
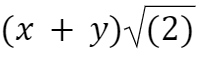
Se applicato agli stati di base di singolo qubit trasforma
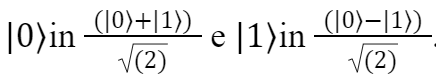
Questo gate quindi fornisce una sovrapposizione coerente tra i due stati di base, che come abbiamo spiegato rappresenta una delle caratteristica fondamentale per la computazione quantistica, anzi per tutta la meccanica quantistica.
Nel campo della computazione quantistica una operazione controllata è una operazione del tipo: “Se la condizione A è vera, esegui B”. Un gate logico fondamentale è il cosiddetto controlled-NOT o CNOT.
Questo gate ha come input due qubit, definiti qubit di controllo e qubit target. Il CNOT agisce sul qubit target e ne inverte lo stato a |1> se il qubit di controllo è |1>, altrimenti lo lascia inalterato. La tavola della verità per il CNOT è la seguente:
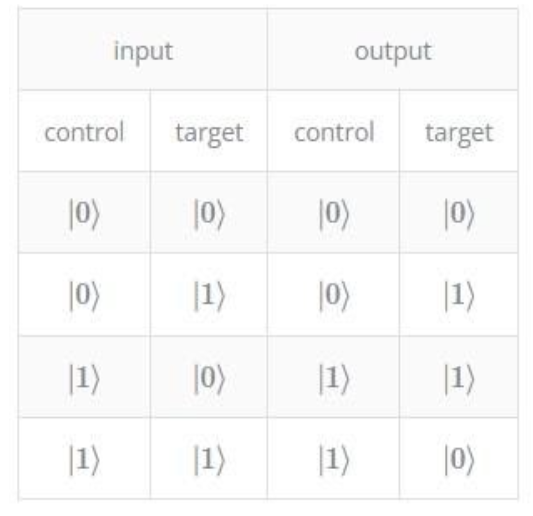
Sappiamo che nella computazione classica un insieme di porte logiche ( ad esempio AND, OR, NOT ) possono essere combinate per potere eseguire una qualsiasi operazione: queste porte sono dette quindi universali. Nella computazione quantistica vale lo stesso principio: esistono set universali di porte logiche quantistiche se ogni operazione unitaria (che sappiamo essere il requisito fondamentale per le porte logiche quantistiche e le matrici che ne danno una rappresentazione) può essere approssimata con precisione arbitraria da un circuito quantistico che contiene quelle porte logiche.
Si può giungere al risultato che le porte necessarie per approssimare ogni operazione unitaria , e quindi ogni gate quantistico, sono i gate di Hadamard, il CNOT, e il gate di phase shift S e T.
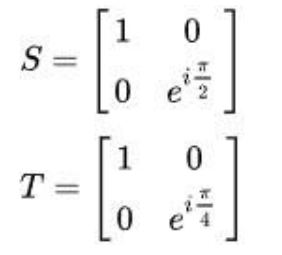
Matrici per i gate di phase shift
Il ruolo e la funzione dei gate quantistici risulteranno più chiari nei capitoli in cui forniremo una panoramica dei vari tipi di computer quantistici e programmeremo il computer IBM.
Nella prossima lezione vedremo come si costruiscono e quali sono i principali algoritmi che si possono implementare sui computer quantistici, e inizieremo a capire quanto l’idea di un calcolatore che basa il suo funzionamento e la sua natura sulla meccanica quantistica sia rivoluzionaria. Intanto possiamo anticipare che i primi algoritmi quantistici sono stati ideati e dimostrati nei primi anni ’90, quando la realizzazione fisica di un computer quantistico era ancora lontana!
Nomi, simboli e matrici associati ai più comuni gate quantistici per singolo qubit
Credits: Quantum Computation and Quantum Information – M. Nielsen, I. L. Chuang
Roberto CampagnolaLo sviluppo di supercomputer per l’intelligenza artificiale sta entrando in una nuova orbita: in termini di scala, costi e consumi energetici e infrastrutture e megaprogetti. Uno studio condotto...
Il 25 Aprile, data simbolo della Liberazione italiana dal fascismo, ci ricorda il valore della libertà, conquistata con il sacrificio di partigiani e combattenti. In un’era dominata dal dig...
In un mondo dove ogni giorno si registrano migliaia di attacchi informatici, molte aziende continuano a sottovalutare l’importanza della cybersecurity, affidandosi a “sedicenti esperti&#x...
AI, AI e ancora AI. E sembra che l’intelligenza artificiale giorno dopo giorno ci porti innovazioni sia come difesa ma soprattutto, come attacco. L’intelligenza artificiale è già...
Il collettivo di ricerca in sicurezza informatica HackerHood, parte dell’universo della community di Red Hot Cyber, ha recentemente scoperto due nuove vulnerabilità ...
Copyright @ REDHOTCYBER Srl
PIVA 17898011006
