Roberto Campagnola : 30 Ottobre 2021 17:24
Autore: Roberto Campagnola
Data Pubblicazione: 30/10/2021
Nel primo articolo abbiamo illustrato i concetti di base e il quadro storico che ha posto le basi per la creazione dell’informatica classica. In questo articolo entriamo nel mondo quantistico, illustrando cosa sono i qubit, la componente fondamentale del processo computazionale che trasmette e contiene l’informazione in un computer quantistico (QC).
CALL FOR SPONSOR - Sponsorizza l'ottavo episodio della serie Betti-RHC
Sei un'azienda innovativa, che crede nella diffusione di concetti attraverso metodi "non convenzionali"?
Conosci il nostro corso sul cybersecurity awareness a fumetti?
Red Hot Cyber sta ricercando un nuovo sponsor per una nuova puntata del fumetto Betti-RHC mentre il team è impegnato a realizzare 3 nuovi episodi che ci sono stati commissionati.
Contattaci tramite WhatsApp al numero 375 593 1011 per richiedere ulteriori informazioni oppure alla casella di posta [email protected]
Supporta RHC attraverso:
Ti piacciono gli articoli di Red Hot Cyber? Non aspettare oltre, iscriviti alla newsletter settimanale per non perdere nessun articolo.
Come i calcolatori classici usano i bit come unità fondamentale dell’informazione, e tali bit si “materializzano” nel passaggio di una corrente in un circuito integrato, così nella computazione quantistica si usano i qubit (Quantum bit).
I metodi sperimentali per costruire i qubit sono molteplici, e più avanti daremo riferimento delle principali architetture di processori per computer quantistici e realizzazioni dei qubit, anche se per semplicità non si può prescindere da una trattazione puramente matematica e più astratta.
Prima di iniziare, dobbiamo però illustrare alcuni concetti fondamentali della meccanica quantistica e della notazione matematiche che si adopera.
Un qualsiasi sistema quantistico può essere descritto da grandezza, chiamato vettore di stato in uno spazio matematico chiamato Spazio di Hilbert, uno spazio vettoriale complesso.
Per descrivere uno stato quantistico si usa la notazione di Dirac, indicando i vettori come
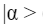
chiamato vettore ket; si postula che tale vettore contenga tutte le informazioni sullo stato fisico del sistema quantistico che stiamo studiando. Associati ai vettori ket, esistono i vettori bra indicati come:
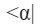
e indicano i vettori a cui è stata applicata l’operazione matematica di coniugazione complessa.
Associata ai vettori di stato, si studia la funzione d’onda, una funzione complessa delle variabili spaziotemporali, tale che il suo modulo elevato al quadrato rappresenta la densità di probabilità di trovare il sistema fisico in un punto dello spazio ad un dato istante.
Tra i postulati fondamentali della meccanica quantistica, ha per noi molto interesse il Principio di sovrapposizione secondo cui due stati quantistici possono essere “sovrapposti”, dando origine ad un ulteriore stato quantisticamente valido.
Date, per esempio due funzioni d’onda:
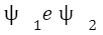
allora anche la funzione d’onda con:
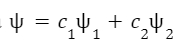
e
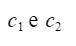
numeri complessi, rappresenta uno stato fisico valido. Vediamo cosa comporta il principio di sovrapposizione nella costruzione dei qubit.
Così come i bit classici possono assumere i valori 0 o 1, anche i qubit possono essere definiti da vettori che li definiscono negli stati:
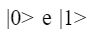
Tra gli stati ammessi possiamo trovare anche una combinazione lineare dei due stati, una sovrapposizione appunto, definita come:
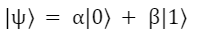
Il qubit descritto da questo stato è simultaneamente, fino al momento della misura o della interazione con l’esterno (possiamo dire finché non è stato svolto il compito per il quale il QC è stato programmato) nello stato 0 e nello stato 1.
I coefficienti che vediamo nella formula. i coefficienti:
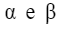
non appartengono al campo dei numeri reali, ma sono coefficienti complessi, e il loro quadrato:
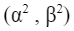
rappresenta la probabilità di ottenere lo stato 0 o lo stato 1, con la condizione che:
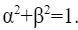
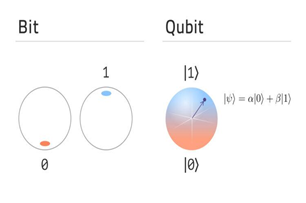
Valori dei bit (sx), e sovrapposizione per i qubit (dx)
E’ questa la differenza rivoluzionaria rispetto ai bit classici, e ciò che rappresenta il punto cardine e la potenza futura dei computer quantistici. I bit classici posso essere o 0 o 1, quindi un registro di n bit può essere in una delle 2^n configurazioni possibili mentre eseguo una serie di calcoli che genereranno un output, anch’esso ben definito tra le 2^n configurazioni possibili.
In in QC invece il mio insieme di qubit, opportunamente impostato, dopo ogni operazione, può essere contemporaneamente al massimo in tutte le 2^n configurazioni, ognuna secondo opportuni pesi. In realtà non sempre è possibile avere i nostri qubit tutti sovrapposti nelle 2^n configurazioni possibili: questo perché alcuni qubit mi potranno servire come qubit di controllo, avendo sempre uno stato definito 0 oppure 1, andando a far diminuire le configurazioni possibili.
Un altro fenomeno che riduce le combinazioni possibili dei qubit è il fenomeno dell’entanglement, di cui parleremo nel prossimo numero della rubrica.
Un modo per rappresentare graficamente il concetto di sovrapposizione di stati per un singolo qubit fa uso della sfera di Bloch, una sfera di raggio unitario i cui punti sulla superficie sono in corrispondenza biunivoca con gli stati del qubit: il “polo nord” rappresenta lo stato
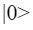
il “polo sud” lo stato
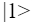
mentre gli altri punti mappano le sovrapposizioni di
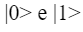
precisamente:
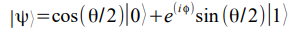
con
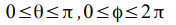
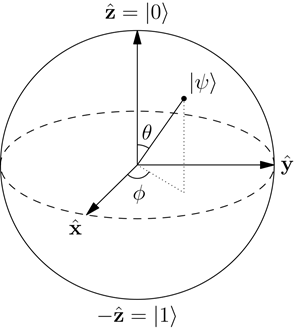
La Sfera di Bloch
Si potrebbe pensare che in un singolo qubit sia contenuta una quantità infinita di informazioni, come potrebbero essere i punti di una sfera. Questa tuttavia è una maniera fuorviante e imprecisa di pensare ai qubit; sappiamo dai postulati della Meccanica Quantistica che nel momento in cui eseguo una misura su un qubit o interagisco con esso ottengo solo 0 oppure 1.
La misura cambia lo stato di un qubit, facendo “collassare” lo stato dalla sovrapposizione di 0 e 1 ad uno stato specifico definito dalle condizioni della misura. Da una singola misura di un qubit ottengo solo un singolo bit di informazione, è fondamentale ricordarlo. Quindi potremmo essere in grado di calcolare i due coefficienti α e β in solo se avessimo infiniti qubit tutti preparati in modo identico.
Questi fenomeni all’apparenza altamente contro intuitivi portano ad una incredibile accelerazione nella computazione di cui parleremo più in dettaglio nel prossimo numero dedicato agli algoritmi quantistici che possono essere utilizzati.
Per una panoramica sulle tecniche per costruire i qubit e i processori dei principali computer quantistici vi rimandiamo a https://www.redhotcyber.com/post/il-processore-del-computer-quantistico.
Reference:
Quantum Computation and Quantum Information – Nielsen, Chuang
Photo credit:
https://en.wikipedia.org/wiki/Bloch_sphere
https://itmanager.space/qubit/
Roberto Campagnola“Combattere il cybercrime è come estirpare le erbacce: se non elimini le radici a fondo, queste ricresceranno” e oggi, più che mai, questa verità si conferma esser...
Immagina di aprire, come ogni sera, il bookmark del tuo forum preferito per scovare nuove varianti di stealer o l’ennesimo pacchetto di credenziali fresche di breach. Invece della solita bachec...
Il 22 luglio 2025, Mozilla ha rilasciato Firefox 141, un aggiornamento volto a migliorare la sicurezza del browser. Nell’ambito del Bollettino MFSA 2025-56, sono state risolte 18 vulnerabilit&#x...
Secondo gli esperti di sicurezza informatica, diversi gruppi di hacker cinesi stanno sfruttando una serie di vulnerabilità zero-day in Microsoft SharePoint nei loro attacchi. In particolare, ...
Un attacco informatico di vasta portata ha violato la National Nuclear Security Administration (NNSA) degli Stati Uniti attraverso il software per documenti Sharepoint di Microsoft, ha confermato...
Iscriviti alla newsletter settimanale di Red Hot Cyber per restare sempre aggiornato sulle ultime novità in cybersecurity e tecnologia digitale.
Copyright @ REDHOTCYBER Srl
PIVA 17898011006
